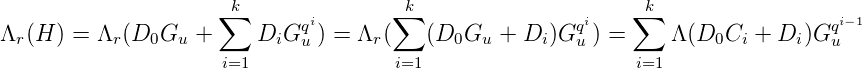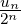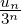Suites automatiques
Xuedong Shang
École Normale Supérieure
26 Janvier 2012
Contents
Nous donnons ici, dans ce petit rapport, un premier traitement, très bref, des suites
engendrées par un automate, modèle le plus simple de machine. Une suite automatique
n’est pas nécessairement très simple ou régulière (ultimement périodique par exemple)
malgré le fait que cela soit dûe à un automate dont les états sont finis. La premère
partie de ce rapport est consacrée à une première aperçu des suites automatiques
avec quelques exemples connus. Puis nous traiterons quelques caractérisations de
l’automaticité en cherchant les liens entre les automates et leurs suite engendrée
associée. À la fin, nous donnerons certains résultats divers sur les suites automatiques.
1 Définitions et exemples
On va commencer par définir la k-automaticité et donner deux exemples de suites 2-automatiques.
Ces suites présenteront des similarité dont les liens seront développés dans la partie
suivante.
Les automates que l’on va utiliser sont déterministes et complets. L’ensemble des états sera
noté Q et au lieu d’avoir certains états finaux on dispose d’une fonction de sortie τ qui à chaque
état associe un valeur "de sortie".
Définition 1. Un automate fini est la donnée de {Q, Σ,δ,i,τ, Γ} où Q est l’ensemble des
états, i ∈ Q est l’état initial, Σ est l’alphabet d’entrée, δ la fonction de transition de Q × Σ
dans Q. Γ l’alphabet de sortie et τ la fonction de sortie de Q dans Γ.
On remarque que pour obtenir un automate usuel, il suffit de prendre Γ = {0, 1} et de
considérer q état final si et seulement si τ(q) = 1. Dans la suite, on n’introduit plus l’alphabet de
sortie Γ dans l’automate s’il n’y pas d’ambiguïté.
Remarque 3. Un tel automate est appelé k-automate, et on peut ainsi dire qu’une suite est
k-automatique si elle est engendrée par un k-automate.
1.1 La suite de Thue-Morse
La suite de Thue-Morse (appelée souvent suite de Prouhet-Thue-Morse chez les francophones) fut
décrite pour la première fois par le mathématicien français Eugène Prouhet en 1851. Il la utilisa
pour donner une solution à un problème de théorie des nombres qui s’appelle le problème de
Prouhet-Tarry-Escott. La suite fut redécouverte par le mathématicien norvégien Axel Thue dans
un article publié en 1906 qui est l’article fondateur de la combinatoire des mots. Puis Marston
Morse, en 1922, donna une nouvelle interprétation de la suite, dans le cadre de la géométrie
différentielle.
Définition 4. On définit la suite de Thue-Morse, (tn)n de la façon suivante :
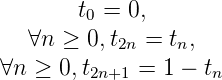
On donne ses premiers termes ci-dessous : 0110100110…
On voit que, d’après la définition de t, tn correspond à la somme des chiffres dans l’écriture en base
2 de n modulo 2. La suite de Thue-Morse est ainsi 2-automatique; elle est engendrée par l’automate
suivant
:
Donnons une autre manière pour définir la suite de Thue-Morse. On considère le morphisme
2-uniforme
σ : {0, 1}* →{0, 1}* donné par :
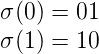
La suite (σn(0))
n converge simplement vers t. Il en résulte que t est point fixe de σ.
1.2 La suite de Rudin-Shapiro
La suite de Rudin-Shapiro, aussi appelée la suite de Golay-Rudin-Shapiro est une suite
automatique nommée par Marcel Golay, Walter Rudin et Harold S.Shapiro, qui l’ont décourvert
indépendemment.
Définition 5. On définit la suite de Rudin-Shapiro (rn)n de la façon suivante :
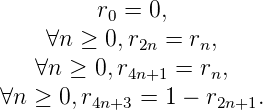
Ses premiers termes sont les suivants : 000100100001…
Il s’agit encore d’une suite 2-automatique. Elle est engendrée par l’automate suivant
:
Cette suite donne le nombre d’occurrences de "11" dans l’écriture de n en base 2, le tout
modulo 2. On ne peut pas trouver comme pour la suite de Thue-Morse un morphisme 2-uniforme
dont la suite soit point fixe. Il faut d’abord "agrandir" l’alphabet. Définissons un morphisme σ sur
l’alphabet {A,B,C,D} par :
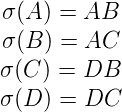
La limite simple de σn(A) est de la forme suivante :
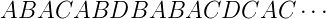
La suite de Rudin-Shapiro s’obtient alors en prenant l’image du point fixe pour σ par la projection
π : {A,B,C,D}→{0, 1} définie par :
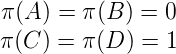
2 Théorème de Cobham
2.1 Le q-noyau
Au niveau des ressemblances entre les deux suites, il est pertinent d’introduire certaines
définitions.
Définition 6. Soit u une suite donnée et k ∈ ℕ. le q-noyau que l’on notera désormais Ku(q) (ou
plus simplement Ku s’il n’y a pas d’ambiguïté) est :
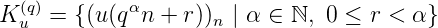
Le q-noyau nous intéresse lorsqu’il n’est pas "trop gros" et qu’il contraint les suites à coïncider
avec leurs propres sous-suites extraites de pas qk. Or il y a au plus un nombre dénombrable de telle
suite, on s’intéresse alors au cas fini.
Lorsque le q-noyau est fini, il est facile de le calculer par machine. Il suffit de construire
récursivement les ensembles Xk donnés par :
![X0 = {(an)n≥0}etXk+1 = Xk ∪ {(bqn+r)n|(bn)n ∈ Xk, r ∈ [0,q - 1]}.](suites_automatiques11x.png) S’il existe k tel que Xk = Xk+1 alors c’est la valeur du q-noyau, ce dernier est alors
fini.
S’il existe k tel que Xk = Xk+1 alors c’est la valeur du q-noyau, ce dernier est alors
fini.
Proposition 7. Le 2-noyau de la suite de Thue-Morse est fini.
Proof. On a
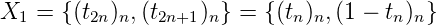
Donc
Kt = {(tn)n, (1 - tn)n} dont le 2-noyau est fini. __
Proposition 8. Le 2-noyau de la suite de Rudin-Shapiro est fini.
Proof. On a
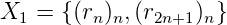
Puis
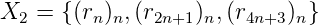
Ensuite
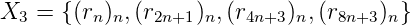
Enfin
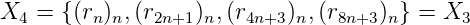
D’où le 2-noyau
Kr = {(rn)n, (r2n+1)n, (r4n+3)n, (r8n+3)n} est fini. __
2.2 Théorème de Cobham
Donnons maintenant un lien avec les morphismes q-uniformes.
Définition 9. Une suite u à valeur dans un alphabet Σ est dite l’image d’un point fixe d’un
point fixe d’un morphisme k-uniforme σ : Σ′ → Σ′ s’il existe w ∈ Σ′ℕ point fixe de σ et π
projection de Σ′ dans Σ tels que ∀n ∈ ℕ,u
n = π(wn).
En écrivant le fait d’être un point fixe lettre à lettre on obtient la caractérisation suivante qui
sera souvent utile.
Lemme 10. Si σ est un morphisme q-uniforme d’un alphabet Σ dans lui même, alors w en est un
point fixe si et seulement si :
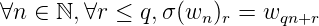
Le lemme est facile à démontrer d’une façon très intuitive. Les deux suites t et r sont image de
point fixe d’un morphisme 2-uniforme. On est à présent en mesure de donner une généralisation
qui porte le nom de Cobham :
Proposition 11 (Cobham, 1972). Soient q ∈ ℕ* et (u
n)n une suite à valeurs dans {0, ,q - 1},
alors les trois assertions suivantes sont équivalentes :
,q - 1},
alors les trois assertions suivantes sont équivalentes :
- la suite (un)n est q-automatique
- le q-noyau Ku de u est fini
- la suite (un)n est image d’un point fixe d’un morphisme q-uniforme
Proof. i) ⇒ ii). On dispose d’un k-automate 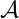 = {Q, Σ,δ,i,τ} qui engendre (un)n. On
rappelle que un = τ(δ(q0,⟨n⟩q)). Or pour i ≥ 0, 0 ≤ j < i, (qin + j)
q = j0…0⟨n⟩q = w⟨n⟩q où
l’on note w = j0i-1. On a alors u
qin+j = τ(δ(q0,w⟨n⟩q)) = τ(δ(δ(q0,w),⟨n⟩q)).
= {Q, Σ,δ,i,τ} qui engendre (un)n. On
rappelle que un = τ(δ(q0,⟨n⟩q)). Or pour i ≥ 0, 0 ≤ j < i, (qin + j)
q = j0…0⟨n⟩q = w⟨n⟩q où
l’on note w = j0i-1. On a alors u
qin+j = τ(δ(q0,w⟨n⟩q)) = τ(δ(δ(q0,w),⟨n⟩q)).
Comme il y a un nombre fini d’états, ainsi que δ(q0,w) selon que i et j varient. Le q-noyau
est alors bien fini.
ii) ⇒ iii). Le q-noyau étant fini supposé de cardinal d, on peut alors écrire Ku =
{(un(1))
n, (un(2))
n,…, (un(d))
n} avec (un(1))
n = (un)n. On définit une suite (V n)n sur l’alphabet
Σd par ∀n ∈ ℕ, V
n = (un(1),u
n(2),…,u
n(d)). Pour j ∈ [0,q - 1], on dispose d’une application
:
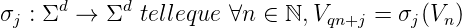
On considère le morphisme
σ : (Σd)* → (Σd)* défini par :
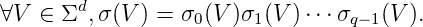
Il est aisé à voir que le morphisme h est q-uniforme, et par le lemme 10, la suite (V n)nest
point fixe de σ. (un)n est l’image de (V n)n par la projection sur la première coordonnée.
iii) ⇒ i). On pose (vn)n = σ∞(v) ,
c’est-à-dire le point fixe de σ où σ est un morphisme q-uniforme sur l’alphabet Σ′ et posons
aussi une application f telle que ∀n,un = f(vn).
Consiérons maintenant l’automate 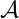 = {Σ′, Σ,δ,v,f} où la fonction de transition δ est
définie par : σ(x) = δ(x, 0)δ(x, 1)
= {Σ′, Σ,δ,v,f} où la fonction de transition δ est
définie par : σ(x) = δ(x, 0)δ(x, 1) δ(x,q - 1). On a alors ∀n ∈ ℕ,un = f(δ(v,⟨n⟩q)). En
effet, on montre par récurrence que :
δ(x,q - 1). On a alors ∀n ∈ ℕ,un = f(δ(v,⟨n⟩q)). En
effet, on montre par récurrence que :
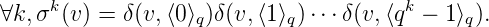
L’initialisation est claire. Pour l’héritage, on a :
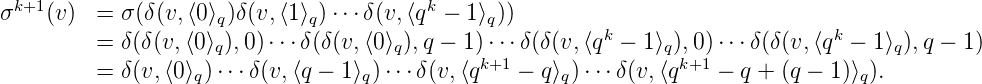
Donc (un)n est bien engendrée par le q-automate 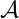 . __
. __
3 Théorème de Christol
Nous présentons dans cette partie un résultat de Gilles Christol. Auparavant, les suites considérées
sont q-automatiques, avec q = pn et p premier. Le théorème donne une caractérisation
surprenante du fait d’être automatique en terme d’algébricité (voir [1]) de série sur le corps
Fq(X).
Plus précisément, le théorème donne une équivalence entre l’algébricité d’une série formelle à
coefficients dans un corps fini et la nature automatique de la suite des coefficients. On va, dans un
premier temps, définir un opérateur qui porte le nom de Cartier.
3.1 Opérateur de Cartier
Notons Fq[[X]] l’ensemble des séries formelles à coefficients dans Fq. Soit u une suite à valeur dans
Fq, on note :
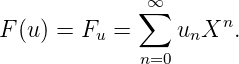
Pour éclaircir l’idée, regardons les deux exemples suivantes:
Exemple 12. On se place dans F2 .
En utilisant la définition de la suite de Thue-Morse t, il vient :
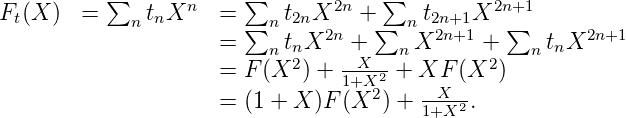
F est donc algébrique sur le corps F2(X) des fractions rationnelles modulo 2. Elle est racine du
polynôme P à coefficients dans F2(X) :
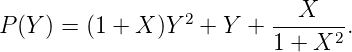
Exemple 13. Par des calculs analogues, on obtient la relation suivante pour la suite de
Rudin-Shapiro r :
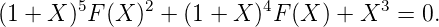
Avant de continuer, il sera utile d’introduire une famille d’opérateurs sur les séries formelles qui
portent le nom de l’opérateur de Cartier.
Définition 14 (Cartier). Soit r ∈{0, ,q - 1}. On définit l’opérateur Λr :
,q - 1}. On définit l’opérateur Λr :
![∑ ∑
Λr : anXn ∈ Fq [[X ]] ↦→ aqn+rXn.
n n](suites_automatiques29x.png)
Le lemme suivant se vérifie facilement.
Lemme 15. Soit r ∈{0, ,q - 1} et F,G ∈ Fq[[X]]. Alors :
,q - 1} et F,G ∈ Fq[[X]]. Alors :
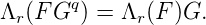
Précisons maintenant ce que veut dire être algégrique sur Fq(X) pour une série formelle
F.
Lemme 16. Soit F = ∑
nanXn une série formelle à coefficients dans F
q, alors F est
algébrique si et seulement si on peut trouver des polynômes B0(X),B1(X), ,Bk(X), non
tous nuls tels que :
,Bk(X), non
tous nuls tels que :
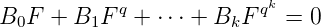 On peut supposer en outre que B0≠0.
On peut supposer en outre que B0≠0.
Proof. Si F est algébrique sur Fq(X), la famille (Fqk)
k≥0 est liée, d’où une relation de
combinaison linéaire non triviale de la forme de l’énoncé. Réciproquement une telle liaison
implique l’algébricité de F. Il reste à montrer que B0 n’est pas nul.
Prenons k ∈ ℕ minimal tel que l’on ait une relation de liaison non triviale comme ci-dessus
et montrons par l’absurde que B0 = 0 :
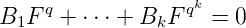
Puis, en utilisant le lemme plus haut :
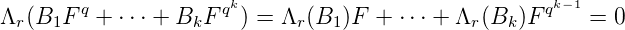
Ce qui contredit alors la minimalité de
k. __
3.2 Théorème de Christol
Théorème 17 (Christol, 1979).
Soit p ≥ 2 un nombre premier et q une puissance de p. Une suite u à valeurs dans Fq est
q-automatique si et seulement si la série formelle F(u) = ∑
nunXn est algébrique sur F
q(X).
Proof. (⇒). Soit u une suite q-automatique. On se servira de l’équivalence prouvée par
Cobham : le q-noyau Ku est fini. Posons alors d = Card(Ku).
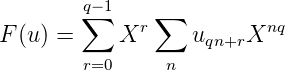
Comme on a dans
Fq,
G(Xq) = G(X)q où
G est un polynôme
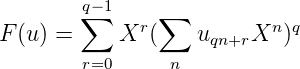
Ce qui montre que :
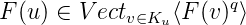
On peut ainsi répéter le processus de la même manière :
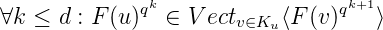
Et donc par une récurrence simple, on obtient :
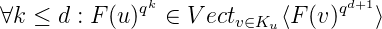
Mais
V ectv∈Ku⟨F(v)qd+1⟩ est de dimension au plus
d, la famille
{F(u),F(u)q, ,F(u)qd}
,F(u)qd}
est liée.
F(u) = ∑
nunXn est donc algébrique sur
F
q(X).
(⇐). Réciproquement, si la série formelle F(u) est algébrique sur Fq(X), d’après le
lemme 16, on peut trouver des polyômes Bi avec B0 non nul tels que :
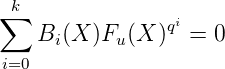
Posons
Gu = Fu∕B0. Il vient
Gu = ∑
i=0kC
iGuqi où
∀i ∈{1,…,k},C
i = -BiB0qi-2.
Posons ensuite
N = max{deg(B0),deg(C1), ,deg(Ck)}
,deg(Ck)} et
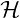
l’ensemble défini par
:
![∑ i
H = {H ∈ Fq[[X ]]|H = ki=0 DiGqu etDi ∈ Fq[X ],deg (Di ) ≤ N }.](suites_automatiques44x.png)
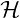 est un ensemble fini contenant Fu. Pour montrer que Ku est fini, il suffit de montrer que ∀r < q,
est un ensemble fini contenant Fu. Pour montrer que Ku est fini, il suffit de montrer que ∀r < q,
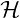 est stable par Λr. Soit alors H un élément de
est stable par Λr. Soit alors H un élément de 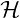 , on a :
, on a :
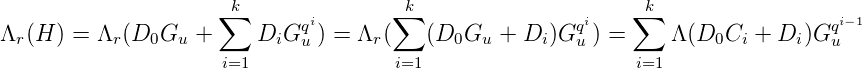
Comme pour tout
i, on a
deg(D0Ci + Di) ≤ deg(D0Ci + Di)∕q ≤ 2N∕q ≤ N, donc
Λr(H) ∈
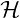
. __
4 Divers
Dans cette partie, nous donnons quelques autres résultats importants sur les suites automatiques.
Cobham a démontré le résultat qui suit dont on trouvera une démonstration dans [2]
:
Théorème 18. Soit k et l deux entiers multiplicativement indépendants
et soit u une suite k et l-automatique, alors u est ultimement périodique.
Corollaire 19. Soit q1 et q2 multiplicativement indépendants et soit u une suite telle que
Fu soit à la fois algébrique sur Fq1 et Fq2, alors u est ultimement périodique.
Proof. En vertu du théorème précédent et celui de Christol. __
En particulier, les suites de Thue-Morse et de Rudin-Shapiro ne sont pas
3-automatiques.
Il est donc intéressant de comparer ce corollaire à la conjecture suivante.
Conjecture 20. Soit (un)n ∈{0, 1}ℕ telle que les deux nombres réels ∑
n∈N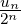 et ∑
n∈N
et ∑
n∈N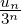 sont algébriques sur ℚ, alors ces deux nombres sont rationnels.
sont algébriques sur ℚ, alors ces deux nombres sont rationnels.
Par ailleurs, on montre que si deux suites u et v à valeurs dans {0,…,q - 1} sont
q-automatiques, leur produit uv l’est aussi. En appliquant le théorème de Christol, on a
:
Corollaire 21. Soient u et v à valeurs dans {0,…,q-1} telles que Fu et Fv sont algébriques
sur Fq(X), alors le produit d’Hadamard
de Fu et Fv est aussi algébrique que l’on note Fuv.
Le lien entre les automates et l’algébricité laisse entrevoir un champ de recherche en théorie des
nombres et en algèbre.
References
[1] J-P.Allouche. Automates et algébricité. In Journal de Théorie des Nombres de
BORDEAUX, volume 17, pages 1–11. Université Bordeaux 1, 2005.
[2] J-P.Allouche and J.Shallit. Automatic sequences, volume 1. Cambridge University
Press, 2003.
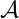 = {Q, Σ,δ,i,τ} tel que :
= {Q, Σ,δ,i,τ} tel que :
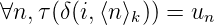
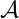 la suite constituée des chiffres de n en base k à partir du chiffre de poids faible, on
tombe sur un état dont la valeur de sortie est un. Il est tout à fait naturel de considérer que la
fonction de sortie est à valeur dans le même ensemble que la suite et que les arêtes de l’automate
sont étiqueées par {0, 1,
la suite constituée des chiffres de n en base k à partir du chiffre de poids faible, on
tombe sur un état dont la valeur de sortie est un. Il est tout à fait naturel de considérer que la
fonction de sortie est à valeur dans le même ensemble que la suite et que les arêtes de l’automate
sont étiqueées par {0, 1, ,k - 1}.
,k - 1}.
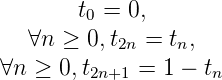

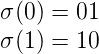
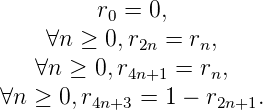
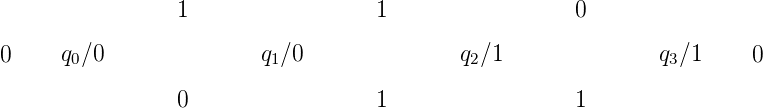
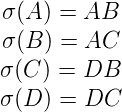
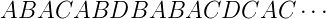
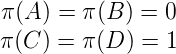
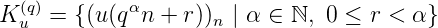
![X0 = {(an)n≥0}etXk+1 = Xk ∪ {(bqn+r)n|(bn)n ∈ Xk, r ∈ [0,q - 1]}.](suites_automatiques11x.png)
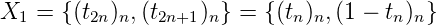
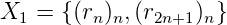
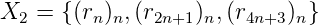
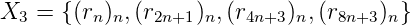
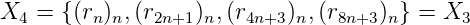
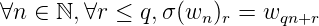

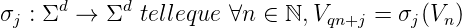
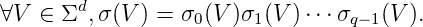

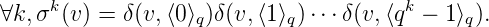
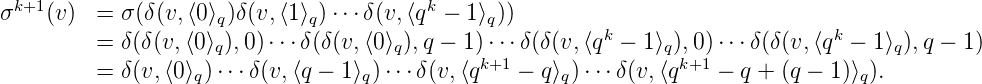
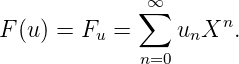
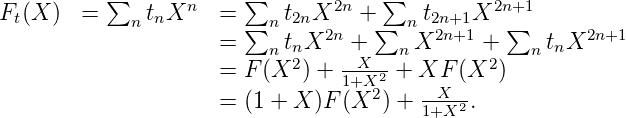
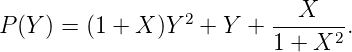
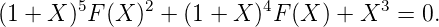

![∑ ∑
Λr : anXn ∈ Fq [[X ]] ↦→ aqn+rXn.
n n](suites_automatiques29x.png)

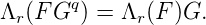

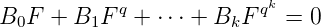
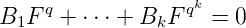
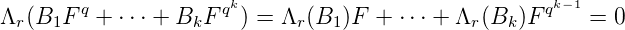
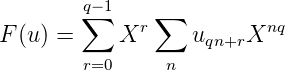
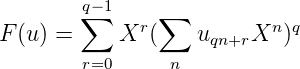
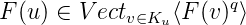
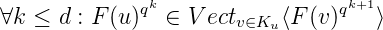
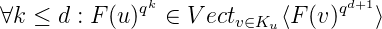

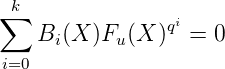

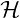
![∑ i
H = {H ∈ Fq[[X ]]|H = ki=0 DiGqu etDi ∈ Fq[X ],deg (Di ) ≤ N }.](suites_automatiques44x.png)